4.0 Introduction
Maps are one of the world’s oldest types of document. For quite some time it was thought that our planet was flat, and during those days, a map simply was a miniature representation of a part of the world. Now that we know that the Earth’s surface is curved in a specific way, we know that a map is in fact a flattened representation of some part of the planet. The field of map projections concerns itself with the ways of translating the curved surface of the Earth into a flat map.
4.1 What is a map projection?
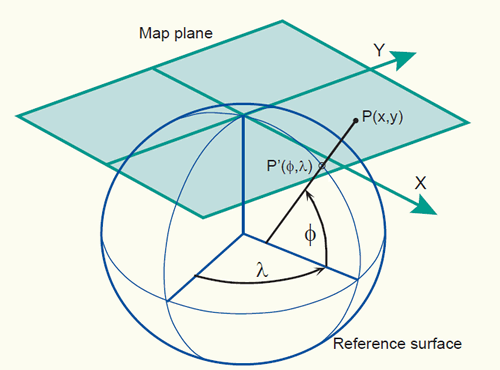
A map projection is a mathematically described technique of how to represent the Earth’s curved surface on a flat map. To represent parts of the surface of the Earth on a flat paper map or on a computer screen, the curved horizontal reference surface must be mapped onto the 2D mapping plane. The reference surface for large-scale mapping is usually an oblate ellipsoid, and for small-scale mapping, a sphere. Mapping onto a 2D mapping plane means transforming each point on the reference surface with geographic coordinates (f,l) to a set of Cartesian coordinates (x,y) representing positions on the map plane (figure below).
Example of a map projection where the reference surface with geographic coordinates (f,l) is projected onto the 2D mapping plane with 2D Cartesian coordinates (x, y).
The actual mapping cannot usually be visualized as a true geometric projection, directly onto the mapping plane as illustrated in the figure above. This is mostly achieved through mapping equations. A forward mapping equation transforms the geographic coordinates (f,l) of a point on the curved reference surface to a set of planar Cartesian coordinates (x,y), representing the position of the same point on the map plane:
(x, y) = f (f, l)
The corresponding inverse mapping equation transforms mathematically the planar Cartesian coordinates (x,y) of a point on the map plane to a set of geographic coordinates (f,l) on the curved reference surface:
(f, l) = f (x, y)
Following are two examples of mapping equations for the sphere (equations for the ellipsoid are generally more complex).
- The first example are the mapping equations used for the Mercator projection:
The forward mapping equation is:
The inverse mapping equation is:
where R is the radius of the spherical reference surface; f and l are given in radians; lo is the central meridian of the projection; e = 2.7182818, the base of the natural logarithms, not the eccentricity.
Suppose a point, located at 60oN and 130oW, is projected on a map that uses the Mercator projection (where the reference surface is a sphere with a radius of 6371000 m. and the central meridian (lo) is 0o, equal to the Greenwich meridian). Using the forward mapping equation of the Mercator projection, the values found for the Cartesian coordinates are for x = -14,455,340m and for y = 8,390,339m.
- The second example is the mapping equations used for the north polar stereographic projection:
The forward mapping equation is:
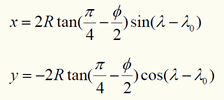
The inverse mapping equation is:
where R is the radius of the spherical reference surface; lo is the longitude of the projection centre.
Suppose the same point, located at 60oN and 130oW, is projected on a map that uses the stereographic projection (where the reference surface is a sphere with a radius of 6371000 m., the centre of the projection is located on the North pole and the longitude of the centre (lo) is 0o). Using the forward mapping equation of the north polar stereographic projection, the values found for the Cartesian coordinates are for x = -2615435m and for y = 2194610m.
Map projection equations have a significant role in projection change (section 5 on coordinate transformations). Interested readers can find an extensive list of mapping equations with numerical examples in 'Map Projections - A Working manual' by J. P. Snyder. A number of equations are also given at World of Mathematics and in the OGP Guidance note 7: Coordinate Conversions and Transformations including Formulas.
4.2 Classification of map projections
Map projections can be described in terms of their:
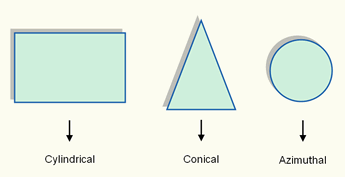
- class (cylindrical, conical or azimuthal),
- point of secancy (tangent or secant),
- aspect (normal, transverse or oblique), and
- distortion property (equivalent, equidistant or conformal).
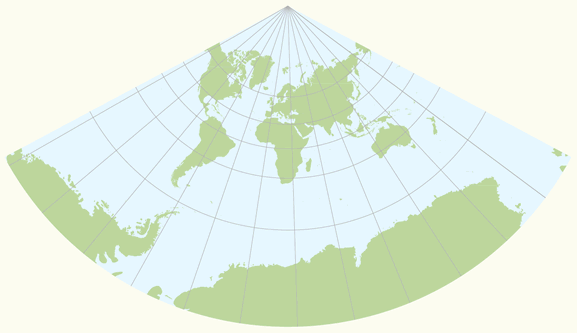
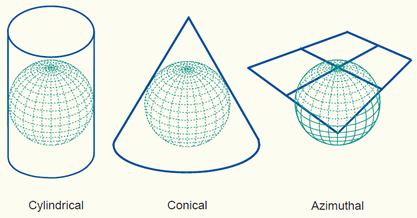
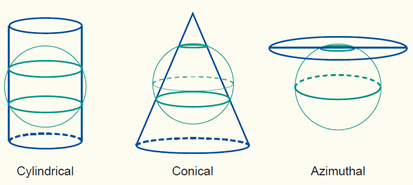
i. The three classes of map projections are cylindrical, conical and azimuthal. The Earth's reference surface projected on a map wrapped around the globe as a cylinder produces a cylindrical map projection. Projected on a map formed into a cone gives a conical map projection. When projected directly onto the mapping plane it produces an azimuthal (or zenithal or planar) map projection. The figure below shows the surfaces involved in these three classes of projections.
The three classes of map projections: cylindrical, conical and azimuthal. The projection planes are respectively a cylinder, cone and plane.
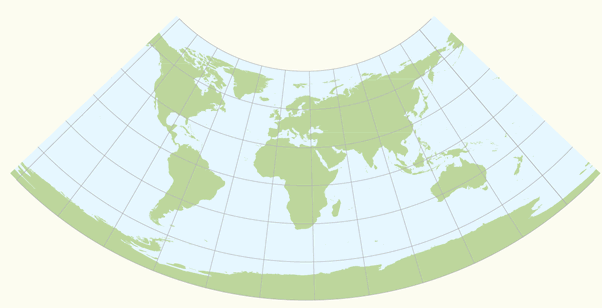
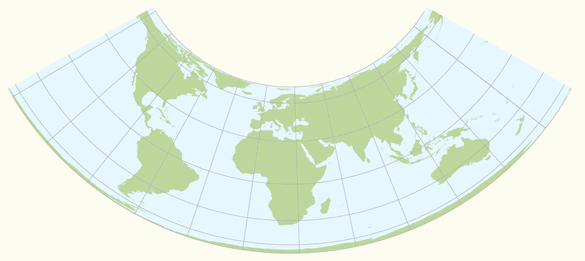
ii. The planar, conical, and cylindrical surfaces in the figure above are all tangent surfaces; they touch the horizontal reference surface in one point (plane) or along a closed line (cone and cylinder) only. Another class of projections is obtained if the surfaces are chosen to be secant to (to intersect with) the horizontal reference surface; illustrations are in the figure below. Then, the reference surface is intersected along one closed line (plane) or two closed lines (cone and cylinder). Secant map surfaces are used to reduce or average scale errors because the line(s) of intersection are not distorted on the map (section 4.3 scale distortions on a map).
Three secant projection classes.
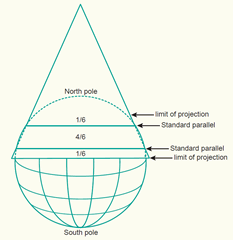
A method to calculate the lines of intersection in a normal conical or cylindrical projection (i.e. standard parallels) could be by determining the range in latitude in degrees north to south and dividing this range by six. The “one-sixth rule” places the first standard parallel at one-sixth the range above the southern boundary and the second standard parallel minus one-sixth the range below the northern limit (figure below). There are other possible approaches.
A conical projection with a secant projection plane. The lines of intersection (standard parallels) are selected at one-sixth below and above the limit of the mapping area.
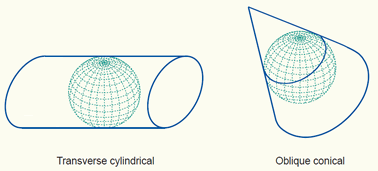
iii. Projections can also be described in terms of the direction of the projection plane's orientation (whether cylinder, plane or cone) with respect to the globe. This is called the aspect of a map projection. The three possible apects are normal, transverse and oblique. In a normal projection, the main orientation of the projection surface is parallel to the Earth's axis (as in the figures above for the cylinder and the cone). A transverse projection has its main orientation perpendicular to the Earth's axis. Oblique projections are all other, non-parallel and non-perpendicular, cases. The figure below provides two examples.
A transverse and an oblique map projection.
The terms polar and equatorial are also used. In a polar azimuthal projection the projection surface is tangent or secant at the pole. In an equatorial azimuthal or equatorial cylindrical projection, the projection surface is tangent or secant at the equator.
iv. So far, we have not specified how the Earth's reference surface is projected onto the plane, cone or cylinder. How this is done determines which kind of distortion properties the map will have compared to the original curved reference surface. The distortion properties of map are typically classified according to what is not distorted on the map:
- In a conformal (orthomorphic) map projection the angles between lines in the map are indentical to the angles between the original lines on the curved reference surface. This means that angles (with short sides) and shapes (of small areas) are shown correctly on the map.
- In an equal-area (equivalent) map projection the areas in the map are identical to the areas on the curved reference surface (taking into account the map scale), which means that areas are represented correctly on the map.
- In an equidistant map projection the length of particular lines in the map are the same as the length of the original lines on the curved reference surface (taking into account the map scale).
A particular map projection can have any one of these three properties. No map projection can be both conformal and equal-area. A projection can only be equidistant (true to scale) at certain places or in certain directions.
Another descriptor of a map projection might be the name of the inventor (or first publisher) of the projection, such as Mercator, Lambert, Robinson, Cassini etc., but these names are not very helpful because sometimes one person developed several projections, or several people have developed similar projections. For example J.H.Lambert described half a dozen projections. Any of these might be called 'Lambert's projection', but each need additional description to be recognized.
Based on these discussions, a particular map projection can be classified. An example would be the classification ‘conformal conic projection with two standard parallels’ having the meaning that the projection is a conformal map projection, that the intermediate surface is a cone, and that the cone intersects the ellipsoid (or sphere) along two parallels; i.e. the cone is secant and the cone’s symmetry axis is parallel to the rotation axis. This would amount to the projection of the figure above (conical projection with a secant projection plane). Other examples are:
- Polar stereographic azimuthal projection with secant projection plane;
- Lambert conformal conic projection with two standard parallels;
- Lambert cylindrical equal-area projection with equidistant equator;
- Transverse Mercator projection with secant projection plane.
4.3 Scale distortions on a map
A map projection without distortions would correctly represent shapes, angles, areas, distances and directions, everywhere on the map. Unfortunately, any map projection is associated with scale distortions. There is simply no way to flatten out a piece of ellipsoidal or spherical surface without stretching some parts of the surface more than others (figure below). The amount and which kind of distortions a map will have depends largely - next to size of the area being mapped - on the type of the map projection that has been selected.
Scale distortions after flattening a piece of the ellipsoidal or spherical reference surface.
Since there is no map projection that maintains correct scale all over the map, it may be important to know the extent to which the scale varies on a map. On a world map, the scale variations are evident where landmasses are wrongly sized or out of shape and the meridians and parallels do not intersect at right angles or are not spaced uniformly. These maps may have a scale reduction diagram to indicate the map scale at different locations, helping the map-reader to become aware of the distortions. On maps at larger scales, maps of countries or even city maps, the distortions are not evident to the eye. However, the map user should be aware of the distortions if he or she computes distances, areas or angles on the basis of measurements taken from these maps.
Scale distortions can be measured and shown on a map by ellipses of distortion. The ellipse of distortion, also known as Tissot's Indicatrix, shows the shape of an infinite small circle with a fixed scale on the Earth as it appears when plotted on the map. Every circle is plotted as circle or an ellipse or, in extreme cases, as a straight line. The size and shape of the ellipse shows how much the scale is changed and in what direction.
The indicatrices on the map in the figure below have a varying degrees of flattening, but the areas of the indicatrices everywhere on the map are the same, which means that areas are represented correctly on the map. The distortion property of the map projection is therefore equal-area (or equivalent).
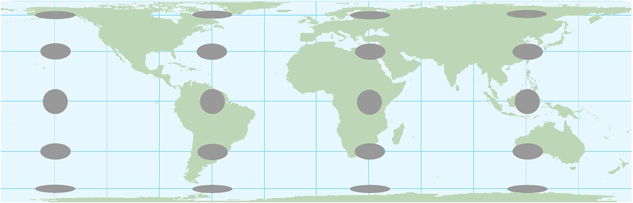
The ellipses of distortion plotted on the cylindrical equal-area projection. The flattening of the ellipses towards the polar regions shows that shape distortions increase towards the polar regions.
When the indicatrices are circles everywhere on the map, the angles and consequently shapes (of small areas) are shown correctly on the map. The distortion property of the map projection is therefore conformal (e.g. the Mercator projection). A Java tool for the demonstration of map projections with an option to show Tissot's indicatrices is given through the following external link:
Demonstration of different map projections (Instituto de matematica, Brasil)
Scale distortions on a map can also be shown by means of a scale factor (ratio of the scale at a given point to the true scale). Scale distortions exist at locations where the scale factor is smaller or larger than 1. E.g. a scale factor at a given point on the map is equal to 0.99960 signifies that 1000 metres on the reference surface of the Earth will actually measure 999.6 metres on the map. This is a contraction of 40 centimetre per kilometre.
The nominal map scale (given map scale) divided by the scale factor will give the actual scale. E.g. a scale factor of 0.99960 at a given point on a map with a nominal scale of 1:10,000 (one to ten thousand) will give a scale of 1:10,004 (10,000 divided by 0.99960) at the given point. This is a smaller scale than the nominal map scale. A scale factor of 2 at a given point on a map with a nominal scale of 1:10M (one to ten million) will give a scale of 1:5M (10 million divided by 2) at the given point. This is a larger scale than the nominal map scale.
Scale distortions for both, tangent and secant map surfaces, are illustrated in the figures below. Distortions increase as the distance from the central point (tangent plane) or closed line(s) of intersection increases.
Scale distortions on a tangent map surface. The central point is not distorted on the map.

Scale distortions on a secant map surface. Line(s) of intersection are not distorted on the map.
On a secant map projection - the application of a scale factor of less than 1.0000 to the central point or the central meridian has the effect of making the projection secant - the overall distortions are less than on one that uses a tangent map surface. Most countries have derived there map coordinate system from a projection with a secant map surface for this reason.
4.4 Choosing a map projection
Every map must begin, either consciously or unconsciously, with the choice of a map projection and its parameters. The cartographer's task is to ensure that the right type of projection is used for any particular map. A well chosen map projection takes care that scale distortions remain within certain limits and that map properties match to the purpose of the map.
Generally, normal cylindrical projections are typically used to map the world in its entirety (in particular areas near the equator are shown well). Conical projections are often used to map the different continents (the mid-latitudes regions are shown well), while the polar azimuthal projections may be used to map the polar areas. Transverse and oblique aspects of many projections can be used for most parts of the world, though they are usually more difficult to construct.
In theory, the selection of a map projection for a particular area can be made on the basis of:
- the shape of the area,
- the location (and orientation) of the area, and
- the purpose of the map.
i.) Ideally, the general shape of the mapping area should match with the distortion pattern of a specific projection. If an area is approximately circular it is possible to create a map that minimizes distortion for that area on the basis of an azimuthal projection. The cylindrical projection is best for a rectangular area and a conic projection for a triangular area (figure below).
The choice of the map projection class (cylindrical, conical or azimuthal) depends largely on the general shape of the mapping area.
ii.) The choice of the aspect of a map projection depends largely on the location (and orientation) of the geographic area to be mapped. Optimal is when the projection centre coincides with centre of the area, or when the projection plane is located along the main axis of the area to be mapped (figure below).
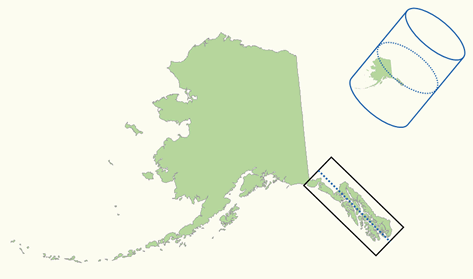
An oblique Mercator projection is used for mapping the Alaska State (zone 5001). The cylindrical projection plane is located along the main axis of the area to be mapped (source: P. H. Dana).
iii.) Once the class and aspect of the map projection have been selected, the distortion property of the map projection has to be chosen. The most appropriate type of distortion property for a map depends largely on the purpose for which it will be used.
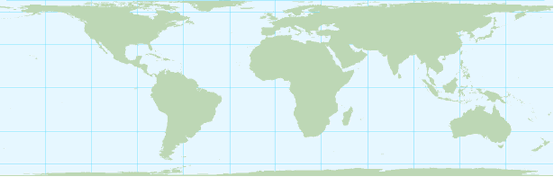
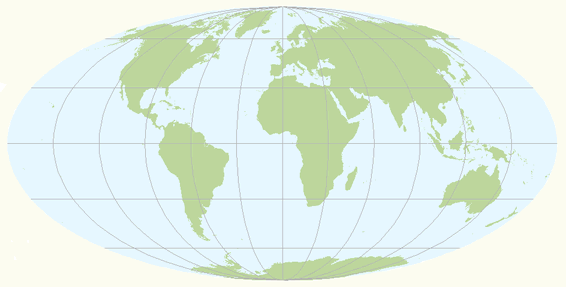
Map projections with a conformal distortion property represent angles and local shapes correctly, but as the region becomes larger, they show considerable area distortions. An example is the Mercator projection. Although Greenland is only one-eighth the size of South America, Greenland appears to be larger (figure below). Maps used for the measurement of angles (e.g. aeronautical charts, topographic maps) often make use of a conformal map projection.
The Mercator projection is a cylindrical map projection with a conformal property. The area distortions are significant towards the polar regions. An example, Greenland appears to be larger but is only one-eighth the size of South America.
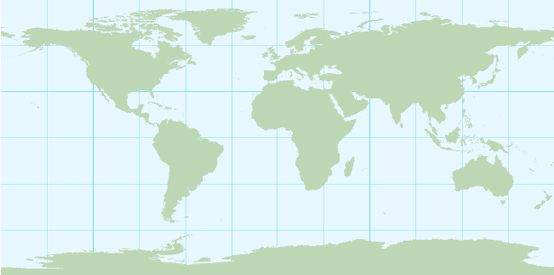
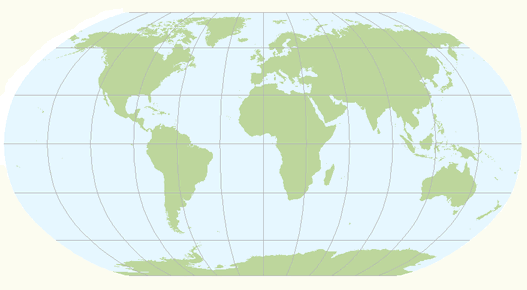
Map projections with a equal-area distortion property on the other hand, represent areas correctly, but as the region becomes larger, it shows considerable distortions of angles and consequently shapes (figure below). Maps which are to be used for measuring areas (e.g. distribution maps) often make use of an equal-area map projection.
The cylindrical equal-area projection after Lambert is a cylindrical map projection with an equal-area property. The shape distortions are significant towards the polar regions.
The equidistant distortion property is achievable only to a limited degree. That is, true distances can be shown only from one or two points to any other point on the map or in certain directions. If a map is true to scale along the meridians (i.e. no distortion in North-South direction) we say that the map is equidistant along the meridians (e.g. the equidistant cylindrical projection in the figure below). If a map is true to scale along all parallels we say the map is equidistant along the parallels (i.e. no distortion in East-West direction). Maps which require correct distances measured from the centre of the map to any point (e.g. air-route, radio or seismic maps) or maps which require reasonable area and angle distortions (several thematic maps) often make use of an equidistant map projection.
The equidistant cylindrical projection (also called Plate Carrée projection) is a cylindrical map projection with an equidistant property. The map is equidistant (true to scale) along the meridians (in North-South direction). Both shape and area are reasonably well preserved with the exception of the polar regions.
In summary, the ideal map projection for any country would either be an azimuthal, cylindrical, or conic projection, depending on the shape of the area, with a secant projection plane located along the main axis of the country or the area of interest. The selected distortion property depends largely on the purpose of the map.
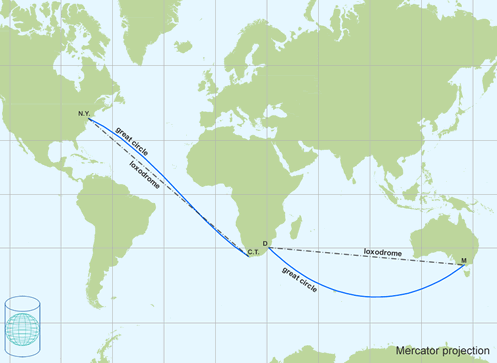
Some map projections have rather special properties. The Mercator projection was originally designed to display accurate compass bearings for sea travel. Any straight line drawn on this projection represents an actual compass bearing. These true direction lines are rhumb lines (or loxodromes). Thus, the route of constant direction between two locations is a always a straight line. For navigation, this is the easiest route to follow, but not necessary the shortes route (figure below).
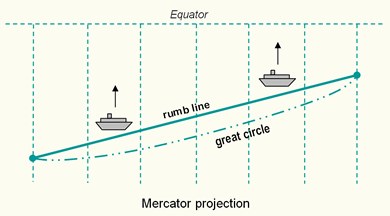
The rhumb lines (lines of constant direction) are shown as straight lines on the Mercator projection. The shortest distance between two points - the great circle path - is shown as a curved line.
The gnomonic projection is a useful projection for defining routes of navigation for sea and air travel, because great circles - the shortest routes between points on a sphere - are shown as straight lines. Thus, the shortest route between any two locations is always a straight line. No other projection has this special property. In combination with the Mercator map where all lines of constant direction are shown as straight lines it assist navigators and aviators to determine appropriate courses. Changes in direction for following the shortest route can be determined by plotting the shortest route (great circle or orthodrome) from the Gnomonic map onto the Mercator map (figure above).
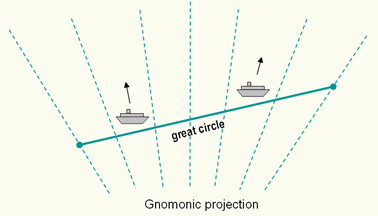
All great circles - the shortest routes between points on a sphere - are shown as straight lines on the gnomonic projection.
In the 15th, 16th and 17th centuries, during the time of great transoceanic voyaging, there was a need for conformal navigation charts. Mercator's projection - conformal cylindrical - met a real need, and is still in use today when a simple, straight course is needed for navigation. Because conformal projections show angles correctly, they are suitable for sea, air, and meteorological charts. This is useful for displaying the flow of oceanic or atmospheric currents, for instance.
For topographic and large-scale maps, conformality and equidistance are important properties. The equidistant property, possible only in a limited sense, however, can be improved by using secant projection planes. The Universal Transverse Mercator (UTM) projection is a conformal cylindrical projection using a secant cylinder so it meets conformality and reasonable equidistance. Other projections currently used for topographic and large-scale maps are the Transverse Mercator (the countries of Argentina, Colombia, Australia, Ghana, S-Africa, Egypt use it) and the Lambert Conformal Conic (in use for France, Spain, Morocco, Algeria). Also in use are the stereographic (the Netherlands) and even non-conformal projections such as Cassini or the Polyconic.
Suitable equal-area projections for thematic and distribution maps include those developed by Lambert, whether azimuthal, cylindrical, or conical. These do, however, have rather noticeable shape distortions. A better projection is the Albers equal-area conic projection with two standard parallels, which is nearly conformal. In the normal aspect, they are excellent for mid-latitude distribution maps and do not contain the noticeable distortions of the Lambert projections.
An equidistant map, in which the scale is correct along a certain direction, is seldom desired. However, an equidistant map is a useful compromise between the conformal and equal-area maps. Shape and area distortions are often reasonably well preserved. An example is the equidistant cylindrical projection (also called Plate Carrée projection), where the meridians are true to scale map (i.e. no distortion in North-South direction).
The projection which best fits a given country is always the minimum-error projection of the selected class. The use of minimum-error projections is however exceptional. Their mathematical theory is difficult and the equidistant projections of the same class will provide a very similar map.
4.5 Map projections in common use
A variety of map projections have been developed, each with its own specfic qualities. Only a limited amount are frequently used. Here are some well-known projections described and illustrated. They are grouped into cylindrical, conical and azimuthal projections.
4.5.1 Cylindrical projections
Probably one of the best known cylindrical projection is Mercator's cylindrical projection. The transverse case and occasionally the oblique case of the Mercator projection are used in several countries for topographic mapping purposes. The Transverse Mercator and Univeral Transverse Mercator (UTM) projection are the best known examples. Two other well-known normal cylindrical projections are the equidistant cylindrical (or Plate Carrée) projection and Lambert's cylindrical equal-area projection. Normal cylindrical projections are typically used to map the world in its entirety (in particular areas near the equator are shown well).
1.Mercator projection:
The Mercator projection is a normal cylindrical projection. The property of the projection is conformal. Parallels and meridians are straight lines intersecting at right angles, a requirement for conformality. Meridians are equally spaced. The parallel spacing increases with distance from the equator (figure below).
Mercator projection is a cylindrical map projection with a conformal property. The loxodromes in black are straight lines. The great circle lines (orthodromes) in blue are curved.
The projection was originally designed to display accurate compass bearings for sea travel. Any straight line drawn on this projection represents a constant compass bearing or a true direction line (loxodrome or rhumb line). Sailing the shortest distance course along the great circle means that the direction changes every moment. These changes in course direction can be deternined by plotting the great circle onto the Mercator projection (figure above).
The Mercator projection is sometimes inappropriately used in atlases for maps of the world, and for wall-maps as area distortions are significant towards the polar regions. The ellipses of distortion appear as circles (indicating conformality) but increase in size away from the equator (indicating area distortion). This exaggeration of area as latitude increases makes Greenland appear to be as large as South America when, in fact, it is only one eight of the size.
The oblique Mercator projection is sometimes used to align the cylindrical projection plane with a region that is oblique and follows neither a north-south nor an east-west axis. For example, this projection is used for mapping the Malaysian peninsula and the Alaska State, zone 5001 (figure section 4.4).
2.Tranverse Mercator projection:
The Transverse Mercator projection is a transverse cylindrical conformal projection. The projection is also known as the Gauss-Krüger or Gauss conformal. Angles and shapes (of small areas) are shown correctly, as a result of conformality. The figure below shows a part of the world mapped on the Transverse Mercator projection.
A part of the world mapped on a transverse cylinder in the Transverse Mercator projection.
Versions of the Transverse Mercator (TM) projection are used in many countries as the local map coordinate system on which the topographic mapping is based. Ghana uses TM projection with the central meridian located at 1°W of Greenwich. The projection is also used for aeronautical charts and recommended to the European Commission for conformal pan-European mapping at scales larger than 1:500,000.
3.Universal Tranverse Mercator (UTM) projection:
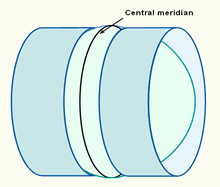
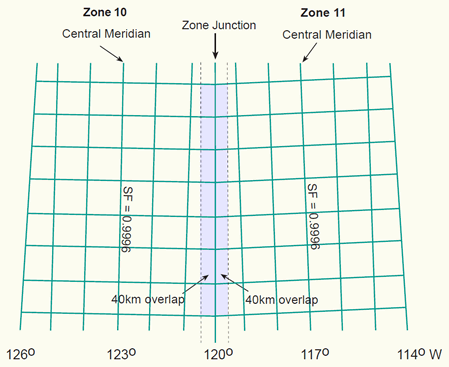
The Universal Transverse Mercator (UTM) projection uses a transverse cylinder, secant to the reference surface (figure below). It is recommended for topographic mapping by the United Nations Cartography Committee in 1952. The UTM divides the world into 60 narrow longitudinal zones of 6 degrees, numbered from 1 to 60. The narrow zones of 6 degrees (and the secant map surface) make the distortions so small that they can be ignored when constructing a map for a scale of 1:10,000 or smaller.
The projection plane of the UTM projection is a secant cylinder in a transverse position.
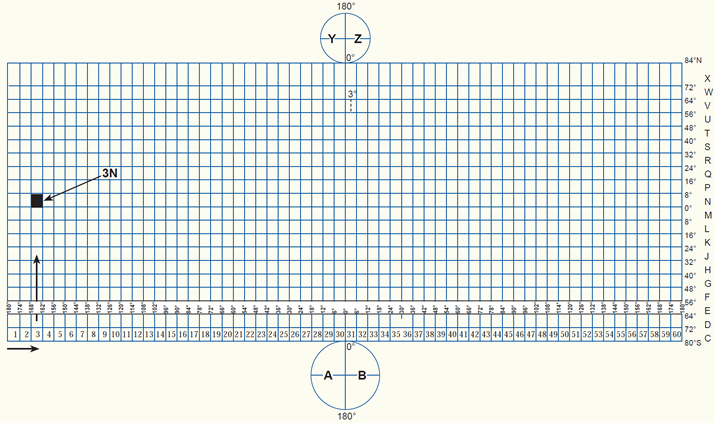
The UTM projection is designed to cover the world, excluding the Arctic and Antarctic regions. The areas not included in the UTM system, regions north of 84°N and south of 80°S, are mapped with the Universal Polar Stereographic (UPS) projection. The figure below shows the UTM zone numbering system. Shaded in the figure is UTM grid zone 3N which covers the area 168° - 162°W (zone number 3), and 0° - 8°N (letter N of the latitudinal belt).
The UTM zone numbering system (click to enlarge).
Each zone has it's own central meridian. E.g. zone 11 extends from 120°W to 114°W, therefore the central meridian has a longitude value of 117°W (figure below).
.gif)
Part of the world mapped in UTM Zone 11. The central meridian is located at 117 degrees west of Greenwich. The zone extends from 120°W to 114°W.
A scale factor of 0.99960 is given to the central meridian of a UTM zone. To avoid negative coordinates for positons located west of the central meridian, the central meridian has been given a (false) Easting value of 500,000m. The equator has been given a Northing value of 0m for positions north of the equator, and a (false) Northing value of 10,000,000m is allocated to the equator for positions south of the equator.
If a map series covers more than one UTM zone it is inconvenient to have the Eastings changing suddenly at a zone junction. For this reason a 40 kilometre overlap into an adjacent zone is allowed (figure below). Mapping beyond this area will result in distortions at the edges of a UTM zone which may not be acceptable for the larger map scales.
2 adjacent UTM-zones of 6 degrees longitude with a 40km overlap into the adjacent zone.
4.Equidistant cylindrical projection:
The equidistant cylindrical projection, also called simple cylindrical, or Plate Carrée, has a true scale along all meridians (i.e. no distortion in north-south direction). The projection is also known as the latitude/longitude projection because the latitude and longitude are directly mapped into y and x respectively. Meridians are spaced at the same distances as the parallels, forming a grid of equal rectangles. Both shape and area are reasonably well preserved with the exception of the polar regions. Used for simple portrayals of the world or regions with minimal geographic data such as index maps. Google Earth uses the equidistant cylindrical (or simple cylindrical) projection for the display of its imagery base. The transverse version of this projection is known as the Cassini projection.
The equidistant cylindrical projection (also called Plate Carrée projection). The map is equidistant (true to scale) along the meridians (in north-south direction). Both shape and area are reasonably well preserved with the exception of the polar regions.
5.Lambert's cylindrical equal-area projection:
The Lambert's cylindrical equal-area projection represents areas correctly, but it does have rather noticeable shape distortions towards the poles. Meridians are equally spaced and 0.32 times the length of the equator. Parallels are unequally spaced and farthest apart near the equator (opposite to the Mercator projection). Because of the distortions it is of little use for world maps. The Mollweide projection, a pseudo-cylindrical equal-area projection, would be a better choice for this purpose. The Gall-Peters projection is a version of Lambert's projection, but with standard parallels at 45 degrees North and South, and also the Behrmann projection, but with standard parallels at 30 degrees North and South.
Lambert's cylindrical equal-area projection. The shape distortions are significant towards the polar regions.
6.Pseudo-cylindrical projections:
Pseudo-cylindrical projections are projections in which the parallels are represented by parallel straight lines, and the meridians by curves. The central meridian is the only meridian that is straight. Examples are Mollweide, Sinusoidal (Sanson-Flamsteed), Goode Homolosine, McBryde-Thomas series, Eckert's series (I -VI), Winkel (I, II), Denoyer and Robinson. They are typically used to map the world in its entirety. Most pseudo-cylindrical projections are equal-area (certainly not conformal because the parallels and meridians do not always cross at right angles).
The Mollweide projection (figure below) is a classic equal-area projection, keeping parallels as straight lines while still preserving areas. All meridians but the central one are elliptical arcs. Suitable for thematic or distribution mapping of the entire world.
Mollweide's pseudo-cylindrical projection with an equal-area property.
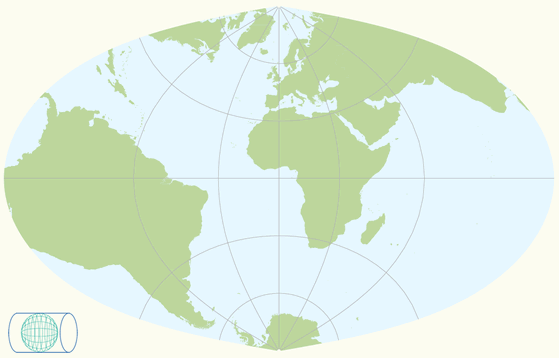
The Robinson projection (figure below) is neither conformal nor equal-area and no point is free of distortion, but the distortions are very low within about 45° of the center and along the Equator and therefore recommended and frequently used for thematic world maps. The projection provides a more realistic view of the world than rectangular maps such as the Mercator.
Robinson's pseudo-cylindrical projection. Shapes and areas are reasonable well preserved.
7.Interrupted projections:
Interrupted projections show the globe in one sheet with interrupted forms of graticules. They are typically used to map the different continents or oceans of the world in one map. Examples are Goode's projection (an interrupted Mollweide projection) or the interrupted Sanson-Flamsteed projection.
Interrupted Mollweide projection for continental masses (after J.P. Goode).
4.5.2 Conic projections
Four well-known normal conical projections are the Lambert conformal conic projection, the simple conic projection, the Albers equal-area projection and the Polyconic projection. They give useful maps of mid-latitudes for countries which have no great extent in latitude.
1.Lambert conformal conic projection:
The Lambert conformal conic projection is confomal. The parallels and meridians intersect at right angles (as in any conformal projection). Areas are, of course, inaccurate in conformal projections. Like with other conformal projections, Lambert's conical is also widely used for topographic maps. It is adapted in France and recommended to the European Commission for conformal pan-European mapping at scales smaller or equal to 1:500,000.
Lambert Conformal Conic projection (standard parallels 10 and 30 degrees North).
2.Simple conic projection:
The simple conic projection (figure below) is a normal conical projection with one standard parallel. All circular parallels are spaced evenly along the meridians, which creates a true scale along all meridians (i.e. no distortion in north-south direction). The map is therefore equidistant along the meridians. Both shape and area are reasonably well preserved. Whereas small countries are possibly shown on this projection, larger areas, such as Russia or Europe are better portrayed on the conic projection with two standard parallels.
Simple conic (or equidistant conic) projection (standard parallel 15 degrees North). The meridians are true to scale.
3.Albers equal-area projection:
The Albers equal-area projection uses two standard parallels. It represents areas correctly and has reasonable shape distortions in the region between the standard parallels as compared with the noticeable distortions of the Lambert's equal-area conic projection with one standard parallel. This projection is best suited for regions predominantly east-west in extent and located in the middle latitudes. Used for small regions or countries but not for continents. It is adapted for maps of the United States, for thematic maps and for world atlases.
Albers equal-area conic projection (standard parallels 10 and 30 degrees North).
5.Polyconic projection:
The polyconic projection is neither conformal nor equal-area. The projection is a derivation from the simple conic projection, but with every parallel true to scale (similar to the Bonne's equal-area projection). The polyconic projection is projected onto cones tangent to each parallel, so the meridians are curved, not straight (figure below). The scale is true along the central meridian and along each parallel. The distortion increase rapidly away from the central meridian. This disadvantage makes the projection unsuitable for large areas on a single sheet. It is adaptable for topographic maps, and is earlier used for the International Map of the World, a map series at 1:1,000,000 scale published by a number of countries to common internationally agreed specifications, and also for large-scale mapping of the United States until the 1950's and coastal charts by the U.S. Coast and Geodetic Survey.
Polyconic projection, with true scale along each parallel.
6.Pseudo-conical projections:
Pseudo-conical projections are projections in which the meridians are represented by curves, and the parallels are equally spaced concentric circular arcs (unlike the pseudo-cylindrical projections in which the parallels are represented by straight lines). The central meridian is the only meridian that is straight. Examples are the Bonne and Werner projection.
Bonne's projection (figure below) is a pseudo-conical equal-area projection, with every parallel true to scale (similar to the polyconic projection). The projection was once popular for large-scale topographic maps and to map the different continents. The Werner projection is a variant of Bonne's projection with the standard parallel at the North or South pole.
Bonne's projection (standard parallel 60 degrees North), with true scale along each parallel.
4.5.3 Azimuthal projections
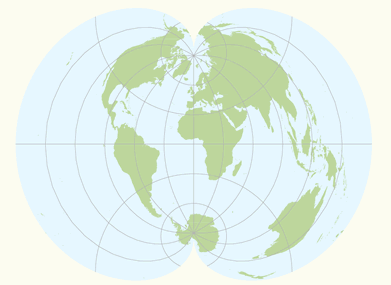
Azimuthal (or zenithal or planar) projections are made upon a plane tangent (or secant) to the reference surface. All azimuthal projections possess the property of maintaining correct azimuths, or true directions from the centre of the map. In the polar cases, the meridians all radiate out from the pole at their correct angular distance apart. A subdivision may be made into perspective and non-perspective azimuthal projections. In the perspective projections, the actual mapping can be visualized as a true geometric projection, directly onto the mapping plane; illustrations are in the figure below. For the gnomonic projection, the perspective point (like a source of light rays), is the centre of the Earth. For the stereographic this point is the opposite pole to the point of tangency, and for the orthographic the perspective point is an infinite point in space on the opposite side of the Earth. Two well known non-perspective azimuthal projections are the azimuthal equidistant projection (also called Postel projection) and the Lambert azimuthal equal-area projection.
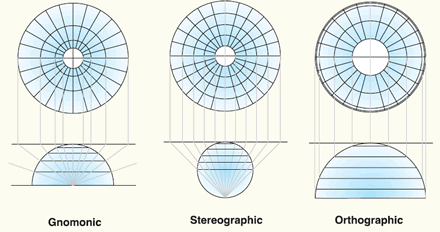
Three perspective azimuthal projections: Gnomonic, stereographic and orthographic (source: ESRI).
1.Stereographic projection:
The azimuthal stereographic projection is a conformal projection. Since the projection is conformal, parallels and meridians intersect at right angles. In the polar aspect the meridians are equally spaced straight lines, the parallels are unequally spaced circles centered at the pole (figure below). Spacing gradually increases away from the pole. The scale is constant along any circle having its centre at the projection centre, but increases moderately with distance from the centre. The ellipses of distortion remain circles (indicating conformality). Areas increase with distance from the projection center. The polar stereographic projection is used in combination with the UTM coordinate system as Universal Polar Stereographic (UPS) for mapping regions north of 84°N and south of 80°S. Recommended for conformal mapping of regions approximately circular in shape; the Netherlands uses a modified version of the stereographic projection (Dutch double stereographic) known as RijksDriehoekstelsel (RD).
Polar azimuthal stereographic projection is a planar projection with a conformal property.
2.Orthographic projection:
The orthographic projection is a perspective projection that views the globe from an infinite distance. Distortion in size and area near the projection limit appears more realistic than almost any other projection. In the polar aspect, meridians are straight lines radiating from the center, and the lines of latitude are projected as concentric circles that become closer toward the edge of the globe. Only one hemisphere can be shown.
Google Earth shows the Earth as it looks from an elevated platform such as an airplane or orbiting satellite. The projection used to achieve this effect is called the general perspective. This is similar to the orthographic projection, except that the point of perspective is a finite (near earth) distance rather than an infinite (deep space) distance.
Polar azimuthal orthographic projection.
3.Gnomonic projection:
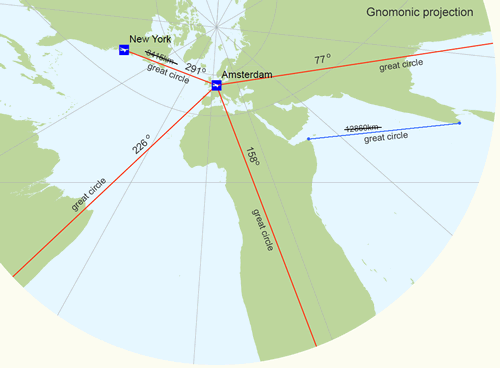
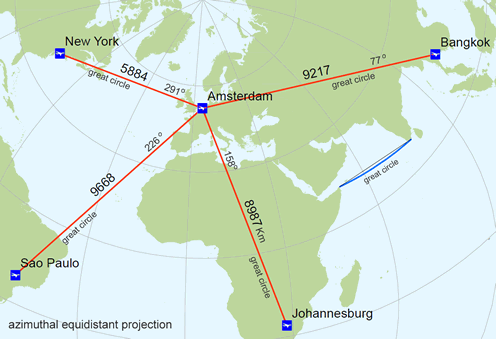
The gnomonic projection (also known as central azimuthal projection) is neither conformal nor equal-area. The scale increases rapidly with the distance from the center. Area, shape, distance and direction distortions are extreme, but all great circles (or orthodromes) - the shortest distances between two places on a sphere - are shown as straight lines. It's wise to orient the centre of the map at the point of interest (figure below), since scale distortions increase rapidly away from the centre of the gnomonic map projection and the direction of the shortest route (azimuth) is shown by a straight line from the centre of the map only (this applies to all azimuthal maps). The projection is useful for defining routes of navigation for sea and air travel, because the shortest route between any two locations is a always a straight line (figure below). It should however not be used for regular geographic maps or for distance measurements. An example, the measured distance on the gnomonic projection between Amsterdam airport and New York airport is 8415 kilometres, but in reality it is around 5884 kilometres (second figure below).
Air-routes plotted in red on a the gnomonic projection. The centre of the projection is oriented at Amsterdam airport. The shortest air-routes - great circle routes - are shown by a straight line and the directions of the shortest air-routes are true from the centre of the projection. However, the distance distortions are extreme.
4.Azimuthal equidistant projection:
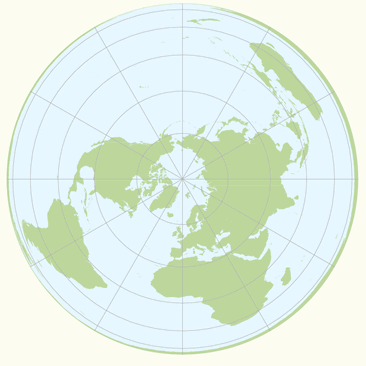
The non-perspective azimuthal equidistant projection (also known as Postel projection) is an equidistant projection. Distances measured from the centre of the map to any point are correct; the bearing of any point from the center is also correct (this applies to all azimuthal maps). Distortion of other properties increases away from the center point, but are not very large compared to the distortions of the gnomonic projection. The projection is frequently used to show air-route distances (figure below).
Air-routes plotted in red on a the azimuthal equidistant projection. The centre of the projection is oriented at Amsterdam airport to show correct distances (and directions) from this point to the other airports. The shortest route - great circle - is shown by a straight line from the centre of the map only (in blue a curved great circle line).
5.Lambert azimuthal equal-area projection:
The non-perspective Lambert azimuthal equal-area projection preserves areas while simultaneously maintaining a true direction from the center. The general pattern of distortion is radial. Scale decreases with distance from the center. It is best suited for maps of continents or regions that are equally extended in all directions from the centre, such as Asia and the Pacific ocean. Recommended to the European Commission for statistical analysis and display. A variant of this projection is the Hammer-Aitoff projection.
Polar azimuthal equal-area projection (after Lambert).
4.6 Map projections overview
In summary, a short list of map projections grouped by class:
List of map projections in common use. See also summary tables on the USGS map projections page.
More examples of map projections are given through the following links:
Demonstration of different map projections (Flex projector, ETH Zurich)
Demonstration of different map projections (Instituto de matematica, Brasil)
Demonstration of different map projections (H. Bottomley)
Map projections grouped by use (Radical cartography)
Picture gallery of map projections (TU Vienna)
Picture gallery of map projections (Nevron)
Understanding map projections (ESRI)
Map projections for Europe (CRSeu)
4.7 Main references
R.A. Knippers. Coordinate systems and Map projections.. Non-published educational notes, ITC, Enschede, 1998.
R.A. Knippers. Geometric Aspects of Mapping. Non-published educational notes, ITC, Enschede, 1999.
P. Stefanovic. Georeferencing and Coordinate Transformations. Non-published educational notes. ITC, Enschede, 1996.
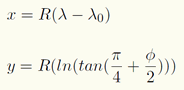
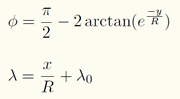
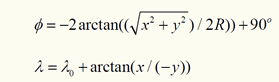

a.gif)
.gif)