1.0 Introduction

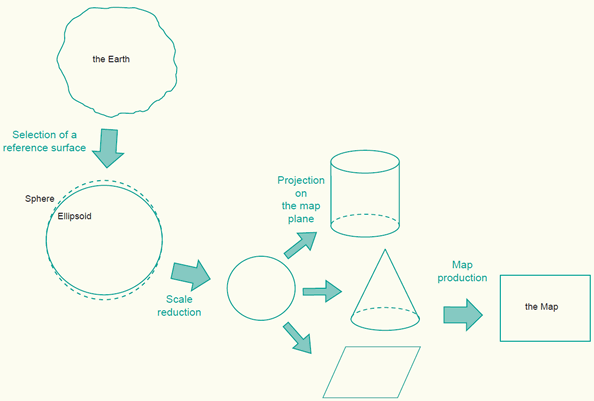
In the process of map making ellipsoidal or spherical surfaces are used to represent the surface of the Earth. These curved reference surfaces are then projected on a map formed into a cylinder, cone or flat plane (figure below). Since a map is a small-scale representation of the Earth's surface it is necessary to apply some kind of scale reduction.

The process of representing the Earth on a flat map.

1.1 Reference surfaces

Two main reference surfaces (or Earth figures) are used to approximate the shape of the Earth. One is called the ellipsoid, the other is the Geoid. The Geoid is the equipotential surface at mean sea level and is used for measuring heights represented on maps. The starting point for measuring these heights are mean sea level points established at coastal places. These points represent an approximation to the Geoid. There are several realizations of local mean sea levels in the world. These are called local vertical datums or height datums.

The ellipsoid (also called spheroid) provides a relatively simple mathematical figure of the Earth. It is used to measure locations, the latitude (f) and longitude (l), of points of interest. These locations on the ellipsoid are then projected onto a mapping plane. There are many different ellipsoids defined in the world, some well-known are the WGS84, GRS80, International 1924 (also known as Hayford), Krasovsky, Bessel, or the Clarke 1880 ellipsoid.

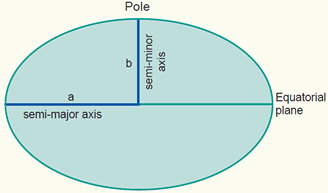
A cross section of an ellipsoid, used to represent the Earth surface, defined by its semi-major axis a and semi-minor axis b. For maps at small scales we can use the mathematically simpler sphere.

 

To measure locations accurately, the selected ellipsoid should fit the area of interest. Therefore a horizontal datum (also called geodetic datum) is established, which is an ellipsoid but positioned and oriented in such a way that it best fits to the area or country of interest. There are a few hundred of these local horizontal datums defined in the world. Recent years have seen that globalisation is leading to the definition of global (or geocentic) datums, such as the ITRF or WGS84.

1.2 Map projections

To produce a map the curved reference surface of the Earth, approximated by an ellipsoid or a sphere, is transformed to the flat plane of the map by means of a map projection. In other words, each point on the reference surface of the Earth with geographic coordinates (f,l) may be transformed to set of Cartesian coordinates (x, y) or map coordinates representing positions on the map plane.

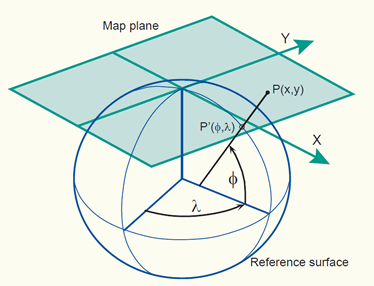
Example of a map projection where the reference surface with geographic coordinates (f,l) is projected onto the 2D mapping plane with 2D Cartesian coordinates (x, y).

 

Hundreds of map projections are developed in order to accurately represent a particular map or to best suit a particular type of map. Examples of map projections are Transverse Mercator (also known as Gauss-Krüger), equidistant cylindrical and conic projection, Lambert's azimuthal, conic and cylindrical projection, stereographic projection, and various others. Map projections are typically classified according to the geometric surface from which they are derived: cylinder, cone or plane. The three classes of map projections are respectively cylindrical, conical and azimuthal.

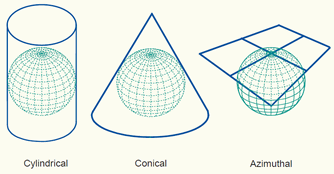
Three classes of map projections.

Furthermore map projections are typically classified according to the distortion properties of a map. The three distortion properties of map projections are respectively: equal-area (or equivalent), equidistant or conformal. Equal-area projections correctly represent area sizes, equidistant map projections correctly represent distances (in certain directions), while conformal map projections correctly represent angles and shapes (of small areas).

1.3 Map coordinate systems

A map coordinate system can be created by choosing a projection and then tailoring its parameters to fit any region on the Earth. An example is the coordinate system used in the Netherlands. It is called Rijksdriehoekstelsel (RD). This 2D Cartesian system is based on the azimuthal stereographic projection centred in the middle of the country and the Bessel ellipsoid is used as reference surface. The horizontal datum, with underlying Bessel ellipsoid, is called Amersfoort datum. The origin of the coordinate system has been shifted (false origin) from the projection centre (Amersfoort) towards the South-West to avoid negative coordinates inside the country.

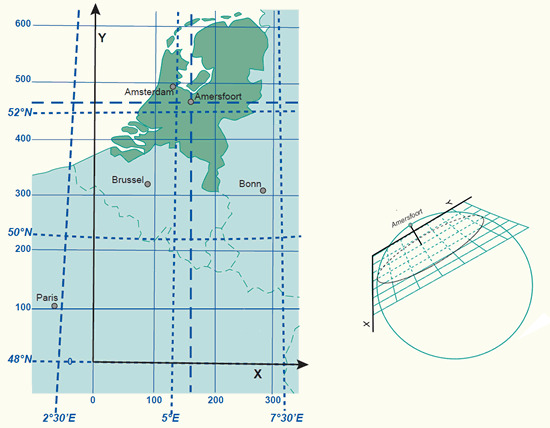
The coordinate system of the Netherlands is derived from an oblique azimuthal stereographic projection.

An overview of map coordinate systems used in the different European countries (external link):

Coordinate Reference Systems for Europe

Standard coordinate systems have been developed to simplify the process of choosing a system. The most important standard map coordinate system used is the Universal Transverse Mercator (UTM). Recent years have seen that globalisation is leading to the establishment of global 3D coordinate systems. These spatial reference systems can be realized thanks to advances in satellite-based positioning. The most important standard 3D system for the GIS community is the International Terrestrial Reference System (ITRS).