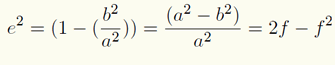3.0 Introduction
The surface of the Earth is anything but uniform. The oceans, can be treated as reasonably uniform, but the surface or topography of the land masses exhibits large vertical variations between mountains and valleys. These variations make it impossible to approximate the shape of the Earth with any reasonably simple mathematical model. Consequently, two main reference surfaces have been established to approximate the shape of the Earth. One reference surface is called the Geoid, the other reference surface is the ellipsoid. These are illustrated in the figure below.
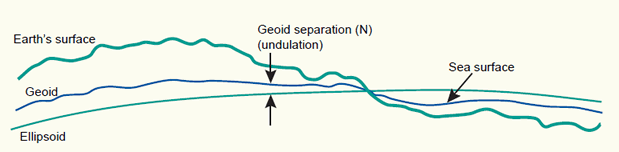
The Earth's surface, and two reference surfaces used to approximate it: the Geoid, and a reference ellipsoid. The deviation between the Geoid and a reference ellipsoid is called geoid separation (N).
3.1 The Geoid and the vertical datum
We can simplify matters by imagining that the entire Earth’s surface is covered by water. If we ignore tidal and current effects on this ‘global ocean’, the resultant water surface is affected only by gravity. This has an effect on the shape of this surface because the direction of gravity - more commonly known as plumb line - is dependent on the mass distribution inside the Earth. Due to irregularities or mass anomalies in this distribution the 'global ocean' results in an undulated surface. This surface is called the Geoid. The plumb line through any surface point is always perpendicular to it.
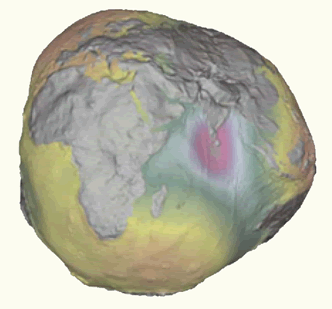
The Geoid, exaggerated to illustrate the complexity of its surface.
Where a mass deficiency exists, the Geoid will dip below the mean ellipsoid. Conversely, where a mass surplus exists, the Geoid will rise above the mean ellipsoid. These influences cause the Geoid to deviate from a mean ellipsoidal shape by up to +/- 100 meters. The deviation between the Geoid and an ellipsoid is called the geoid separation (N) or geoid undulation. The biggest presently known undulations are the minimum in the Indian Ocean with N = -100 meters and the maximum in the northern part of the Atlantic Ocean with N = +70 meters (figure below).
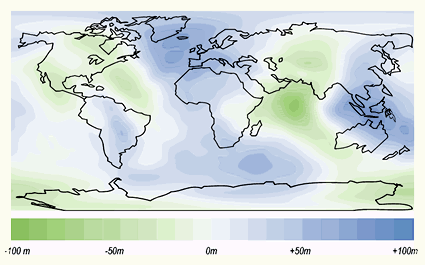
Deviations (undulations) between the Geoid and the WGS84 ellipsoid.
Tool for the calculation of a geoid undulation (compared to WGS84) at a point whose latitude and longitude is specified (external link):
The Geoid is used to describe heights. In order to establish the Geoid as reference for heights, the ocean’s water level is registered at coastal places over several years using tide gauges (mareographs). Averaging the registrations largely eliminates variations of the sea level with time. The resulting water level represents an approximation to the Geoid and is called the mean sea level.
Every nation or groups of nations have established those mean sea level points, which are normally located close to the area of concern. For the Netherlands and Germany, the local mean sea level is realized through the Amsterdam tide-gauge (zero height). We can determine the height of a point in the Netherlands or Germany with respect to the Amsterdam tide gauge using a technique known as geodetic levelling (figure (b) below). The result of this process will be the height above local mean sea level. The height determined with respect to a tide-gauge station is known as the orthometric height (height H above the Geoid).
Obviously, there are several realizations of local mean sea levels (also called local vertical datums) in the world. They are parallel to the Geoid but offset by up to a couple of meters. This offset is due to local phenomena such as ocean currents, tides, coastal winds, water temperature and salinity at the location of the tide-gauge.
Care must be taken when using heights from another local vertical datum. This might be the case in the border area of adjacent nations. An example, the tide gauge (zero height) of the Netherlands differs -2.34 metres from the tide gauge (zero height) of the neighbouring country Belgium (figure below). Even within a country, heights may differ depending on to which tide gauge, mean sea level point, they are related. An example, the mean sea level from the Atlantic to the Pacific coast of the USA increases by 0.6 to 0.7m.
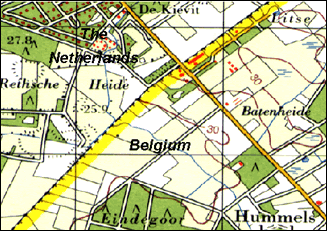
Fragment of a topographic map showing the border area of Belgium and the Netherlands. The heights in both countries refer to different tide gauges (zero heights). As a result, height contours (represented by brown lines) are abruptly ending at the border.
The local vertical datum (or height datum) is implemented through a levelling network (figure (a) below). A levelling network consists of benchmarks, whose height above mean sea level has been determined through geodetic levelling. The implementation of the datum enables easy user access. The surveyors do not need to start from scratch (i.e. from the Amsterdam tide-gauge) every time they need to determine the height of a new point. They can use the benchmark of the levelling network that is closest to the point of interest (figure (b) below).
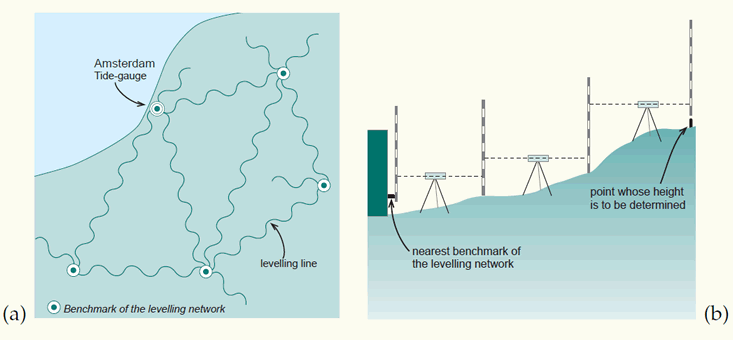
A levelling network implements a local vertical datum: (a) network of levelling lines starting from the Amsterdam tide-gauge, showing some of the benchmarks; (b) how the orthometric height (H) is determined for a point, working from the nearest benchmark.
The use of satellite-based positioning equipment (e.g. GPS) to determine heights with respect to a reference ellipsoid (e.g. WGS84) is becoming more in use. These heights are known as the ellipsoidal heights (height h above the ellipsoid). Ellipsoidal heights have to be adjusted before they can be compared to orthometric (mean sea level) heights. Geoid undulations (N) are used to adjust the ellipsoidal heights (H = h - N).
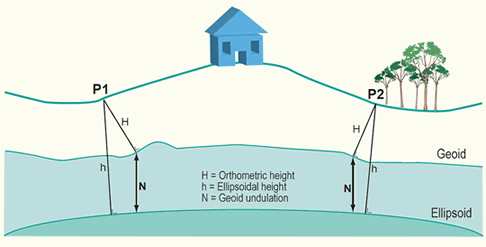
Height h above the reference ellipsoid and height H above the Geoid for two points on the Earth surface. The ellipsoidal height is measured orthogonal to the ellipsoid. The orthometric height is measured orthogonal to the Geoid.
As a result of satellite gravity missions, it is currently possible to determine the orthometric height (height H above the Geoid) with centimetre level accuracy. It is foreseeable that a global vertical datum may become ubiquitous in the next 10-15 years. If all published maps are also using this global vertical datum by that time, heights will become globally comparable, effectively making local vertical datums redundant for GIS users.
3.2 The ellipsoid
Above, we have defined a physical surface, the Geoid, as a reference surface for heights. We also need a reference surface for the description of the horizontal coordinates (i.e. geographic coordinates) of points of interest. Since we will later project these horizontal coordinates onto a mapping plane, the reference surface for horizontal coordinates requires a mathematical definition and description. The most convenient geometric reference is the oblate ellipsoid (figure below). It provides a relatively simple figure which fits the Geoid to a first order approximation, though for small scale mapping purposes a sphere may be used. An ellipsoid is formed when an ellipse is rotated about its minor axis. This ellipse which defines an ellipsoid or spheroid is called a meridian ellipse (notice that ellipsoid and spheroid are used here as equivalent and interchangeable words).
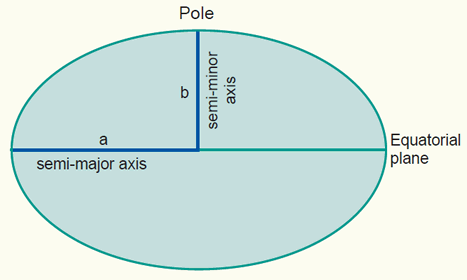
An oblate ellipse, used to represent the Earth surface, defined by its the semi-major axis a and semi-minor axis b.
The shape of an ellipsoid may be defined in a number of ways, but in geodetic practice the definition is usually by its semi-major axis a and flattening. Flattening f is dependent on both the semi-major axis a and the semi-minor axis b.
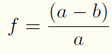
The ellipsoid may also be defined by its semi-major axis a and eccentricity e, which is given by:
Given one axis and any one of the other three parameters, the other two can be derived. Typical values of the parameters for an ellipsoid are:
![]()
3.3 The sphere
As can be seen from the dimensions of the Earth ellipsoid, the semi-major axis a and the semi-minor axis b differ only by a bit more than 21 kilometres (figure below). A better impression on the Earth's dimensions may be achieved if we refer to a more "human scale". Considering a sphere of approximately 6 metre in diameter then the ellipsoid is derived by compressing the sphere at each pole by 1 cm only. This compression is rather small compared to the dimension of the semi-major axis a.
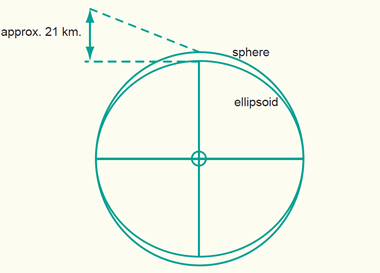
The sphere compared to the ellipsoid.
The consequence is that instead of using the ellipsoid, the sphere might be sufficient for certain mapping tasks. In practice, maps at scale 1:5,000,000 or smaller can use the mathematically simpler sphere without the risk of large distortions. At larger scales, the more complicated mathematics of ellipsoids are needed to prevent these distortions in the map.
The mathematically simpler sphere may be used as reference surface for maps at small-scale.
3.4 Local and global ellipsoids
Many different ellipsoids have been defined in the world. Local ellipsoids have been established to fit the Geoid (mean sea level) well over an area of local interest, which in the past was never larger than a continent. This meant that the differences between the Geoid and the reference ellipsoid could effectively be ignored, allowing accurate maps to be drawn in the vicinity of the datum (figure below).
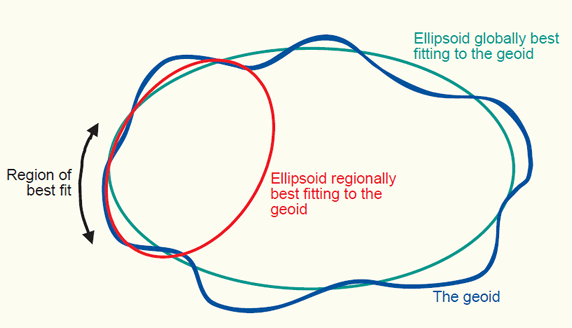
The Geoid, a globally best fitting ellipsoid for it, and a regionally best fitting ellipsoid for it, for a chosen region.
With increasing demands for global surveying, work is underway to develop global reference ellipsoids. In contrast to local ellipsoids, which apply only to a specific country or localized area of the Earth’s surface, global ellipsoids approximate the Geoid as a mean Earth ellipsoid. The International Union for Geodesy and Geophysics (IUGG) plays a central role in establishing these reference figures.
In 1924, the general assembly of the IUG in Madrid introduced the ellipsoid determined by Hayford in 1909 as the International ellipsoid. However, according to present knowledge, the values for this Earth model give an insufficient approximation.
At the general assembly 1967 of the IUGG in Luzern, the 1924 reference system was replaced by the Geodetic Reference System 1967 (GRS 1967). It represents a good approximation (as of 1967) to the mean Earth figure.
For some time, the Geodetic Reference System 1967 was used in the planning of new geodetic surveys. For example, the Australian Datum 1966 and the South American datum 1969 are based upon this ellipsoid. However, at its general assembly 1979 in Canberra the IUGG recognized that the Geodetic Reference System 1967 no longer represented the size and shape of the Earth to an adequate accuracy. Consequently, it was replaced by the Geodetic Reference System 1980 (GRS80) ellipsoid.

Three global ellipsoids defined by a semi-major axis a, semi-minor axis b, and flattening f. The GRS80 and WGS84 can be considered identical for all practical purposes.
3.5 The local horizontal datum
Ellipsoids have varying position and orientations. An ellipsoid is positioned and oriented with respect to the local mean sea level (or Geoid) by adopting a latitude (f ) and longitude (l) and ellipsoidal height (h) of a so-called fundamental point and an azimuth to an additional point. We say that this defines a local horizontal datum. Notice that the term horizontal datum and geodetic datum are being treated as equivalent and interchangeable words.
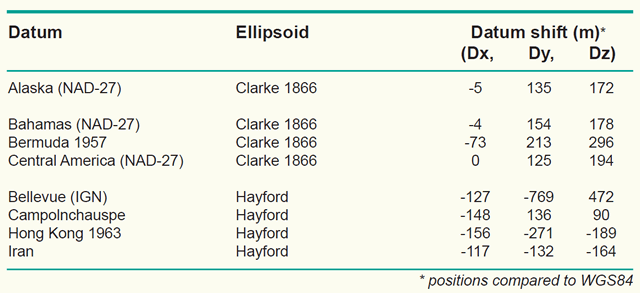
Examples of local horizontal datums with their underlying ellipsoid and difference in position (datum shift) with respect to WGS84.
Several hundred local horizontal datums exist in the world. The reason is obvious: Different local ellipsoids with varying position and orientation had to be adopted to best fit the local mean sea level in different countries or regions. An example is the Potsdam Datum, the local horizontal datum used in Germany. The fundamental point is in Rauenberg and the underlying ellipsoid is the Bessel ellipsoid (a = 6,377,397,156 m, b = 6,356,079.175 m). We can determine the latitude and longitude (f, l) of any other point in Germany with respect to this local horizontal datum using geodetic positioning techniques, such as triangulation and trilateration. The result of this process will be the geographic (or horizontal) coordinates (f, l) of the new point in the Potsdam Datum. Other examples of local horizontal datums (or geodetic datums) are the North American Datum 1927 is used for the North American countries, the Tokyo Datum for Japan, the European Datum for the European countries, and the Amersfoort datum for the Netherlands.
The local horizontal datum is realized through a so-called triangulation network (or survey network). Such a network consists of monumented points forming a network of triangular mesh element (figure below). The angles in each triangle are measured in addition to at least one side of a triangle; the fundamental point is also a point in the triangulation network. The angle measurements and the adopted coordinates of the fundamental point are then used to derive geographic (or geodetic) coordinates (f, l) for all monumented points of the triangulation network.
Within this framework, users do not need to start from scratch (i.e. from the fundamental point) in order to determine the geographic coordinates of a new point. They can use the monument of the triangulation network that is closest to the new point. The extension and re-measurement of the network is nowadays done through satellite measurements.
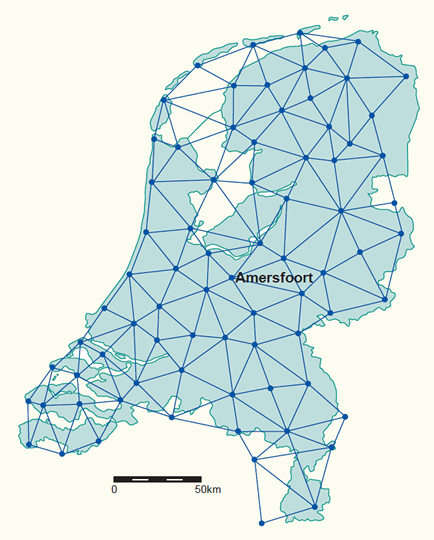
The old primary triangulation network in the Netherlands made up of 77 points (mostly church towers). The extension and re-measurement of the network is nowadays done through satellite measurements (click for town names).
Computations of a triangulation network for a local horizontal datum were usually made with optical survey instruments such as a theodolite or total station. These instruments are levelled by means of spirit bubbles. The bubbles follow the influence of the Earth's gravity which means that the computations have to be corrected with respect to the ellipsoid. Without these corrections the computations may be distorted by some centimeters or even decimeters because of the local difference between the direction of the plumb line (the normal to the Geoid) and the vertical direction on the ellipsoid (the normal to the ellipsoid). This difference in direction is known as the deflection of the vertical (figure below). Gravity measurements are used to determine these vertical deflections. Satellite-based measurements (e.g. GPS) are not involved with these vertical deflections, because the GPS receiver directly relates the measurements to the reference ellipsoid.
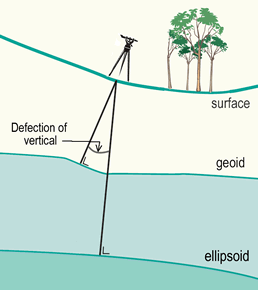
The angle between normal to the Geoid and the normal to the ellipsoid is known as the deflection of the vertical (the angle is exaggerated to illustrate it). Vertical deflections are caused by Geoid undulations and amount to 10" (flat areas) or 20-50" (steep mountain slopes).
3.6 The global horizontal datum
Local horizontal datums have been established to fit the Geoid well over the area of local interest, which in the past was never larger than a continent. With increasing demands for global surveying activities are underway to establish global reference surfaces. The motivation is to make geodetic results mutually comparable and to provide coherent results also to other disciplines like astronomy and geophysics.
The most important global (or geocentric) spatial reference system for the GIS community is the International Terrestrial Reference System (ITRS). It is a three-dimensional coordinate system with a well-defined origin (the centre of mass of the Earth) and three orthogonal coordinate axes (X,Y,Z). The Z-axis points towards a mean Earth north pole. The X-axis is oriented towards a mean Greenwich meridian and is orthogonal to the Z-axis. The Y-axis completes the righthanded reference coordinate system (figure (a) below).
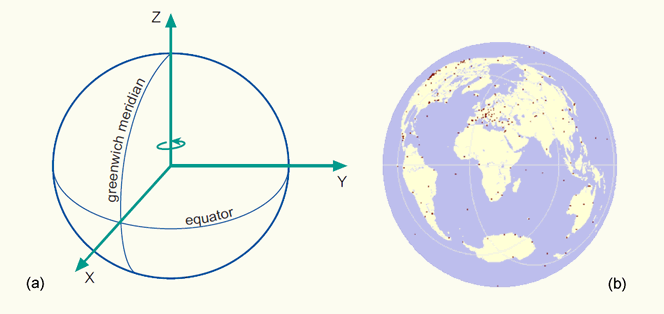
(a) The International Terrestrial Reference System (ITRS), and; (b) the International Terrestrial Reference Frame (ITRF) visualized as a distributed set of ground control stations (represented by red points).
The ITRS is realized through the International Terrestrial Reference Frame (ITRF), a distributed set of ground control stations that measure their position continuously using GPS (figure (b) above). Constant re-measuring is needed because of the involvement of new control stations and ongoing geophysical processes (mainly tectonic plate motion) that deform the Earth’s crust at measurable global, regional and local scales. These deformations cause positional differences in time, and have resulted in more than one realization of the ITRS. Examples are the ITRF96 or the ITRF2000 datums.
The ITRF96 datum was established at the 1st of January, 1997. This means that the measurements use data up to 1996 to fix the geocentric coordinates (X,Y and Z in metres) and velocities (positional change in X,Y and Z in metres per year) at the different stations. The velocities are used to propagate the measurements to other epochs (times). The trend is to use the ITRF everywhere in the world for reasons of global compatibility. The World Geodetic System of 1984 (WGS84) datum has been refined on several occasions and is now aligned with the ITRF to within a few centimetres worldwide. The Global Positioning System (GPS) uses the WGS84 as its reference system.
Global horizontal datums, such as the ITRF2000 or WGS84, are also called geocentric datums because they are geocentrically positioned with respect to the centre of mass of the Earth. They became available roughly after the 1960's, with advances in extra-terrestrial positioning techniques. These techniques include Satellite Laser Ranging (SLR), Lunar Laser Ranging (LLR), Global Positioning System (GPS), and Very Long Baseline Interferometry (VLBI), among others. Since the size and shape of satellite orbits is directly related to the centre of mass of the Earth, observations of natural or artificial satellites can be used to pinpoint the centre of mass of the Earth, and hence the origin of the ITRS. This technique can also be used for the realization of the global ellipsoids and datums at the accuracy level required for large-scale mapping.
To implement the ITRF in a region, a densification of control stations is needed to ensure that there are enough coordinated reference points available in the region. These control stations are equipped with permanently operating satellite positioning equipment (i.e. GPS receivers and auxiliary equipment) and communication links. Examples for (networks consisting of) such permanent tracking stations are the AGRS in the Netherlands and the SAPOS in Germany.
We can easily transform ITRF coordinates (X,Y and Z in metres) into geographic coordinates (f,l,h) with respect to the GRS80 ellipsoid without the loss of accuracy. However, the ellipsoidal height h, obtained through this straightforward transformation, is has no physical meaning and contrary to our intuitive human perception of height. Therefore we use the height H, above the Geoid (figure below). It is foreseeable that global 3D spatial referencing, in terms of (f,l,H), could become ubiquitous in the next 10–15 years. If all published maps are also globally referenced by that time, the underlying spatial referencing concepts will become transparent and hence redundant for GIS users.
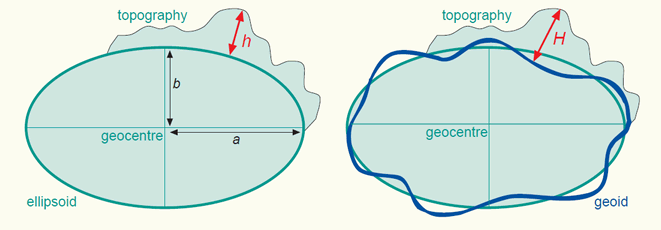
Height h above the geocentric ellipsoid, and height H above the Geoid. The first is measured orthogonal to the ellipsoid, the second orthogonal to the Geoid.
Hundreds of existing local horizontal and vertical datums are still relevant because they form the basis of map products all over the world. For the next few years, we will be required to deal with both local and global datums until the former are eventually phased out. During the transition period, we will require tools to transform coordinates from local horizontal datums to a global horizontal datum and vice versa (section 5 on coordinate transformations). The organizations that usually develop transformation tools and make them available to the user community are provincial or National Mapping Organizations (NMOs) and cadastral authorities.
3.7 Main references
de By, R.A. (editor), Georgiadou, P.Y., Knippers, R.A., Kraak, M.J., Sun, Y., Weir, M.J.C. and van Westen, C.J. Principles of geographic information systems (Chapter 4.2 on spatial referencing), 2nd edition, ITC Educational Textbook, ITC, Enschede, 2001.
A. Mehlbreuer. Geometric Fundamentals of Mapping. Non-published educational notes, ITC, Enschede.
R.A. Knippers. Geometric Aspects of Mapping. Non-published educational notes, ITC, Enschede, 1999.
P. Stefanovic. Georeferencing and Coordinate Transformations. Non-published educational notes. ITC, Enschede, 1996.